This model examines the dynamics of stem cells (Planarian neoblasts) that are allowed to reproduce and migrate within a morphologically complex animal. Distinct neoblast lineages are assumed to respond differently to large-scale morphological signals and to compete; the model examines the conditions under which such differential responsiveness to signals and inter-lineage competition is compatible with neoblast population stability or leads to chaos, runaway inter-lineage competition and cell death. The structure and behavior of the model are described in more detail below.
The model depicts a two-dimensional array of "cells" representing small voxels of a planarian body. Each cell is occupied by neoblasts with lineages indicated by a particular color.Bright colors (R, G, B, C, M, Y) represent areas occupied by a single lineage; intermediate colors represent areas occupied by mixtures of lineages. Rapid switching between colors indicates unstable winner-take-all competition between lineages. Black squares indicate areas in which all neoblasts have been driven to zero population, i.e. areas of cell death.
The 40 X 30 cell grid shown has toroidal topology: cells along the top and bottom borders are neighbors, and cells on the left and right borders are neighbors. This topology gives every cell four abutting neighbors. Note that the word "cell" here is used to indicate a grid cell in the model, not a biological stem cell. The term "neoblast" is used for stem cells.
Each cell is initialized to a random mixture of neoblast lineages, indicated by a random mixture of red, green and blue color. On each time step, each cell calculates the difference between its mixture of lineages and the average mixture of its neighbors, and adjust its mixture toward the average of its neighbors by 1/4 of this difference (i.e. the nearest-neighbor convergence rate = 0.25). This convergence to uniformity models low-level, unbiased competition between lineages located in a single morphological region. The averaging process is inhibited if one of a cell's neighbors has one pure lineage and another of its neighbors has a different pure lineage. This inhibition creates a mixed-lineage boundary between regions with different pure lineages.
"Initiate random migrations" adds, with the probability specified (default = 10%), one long range migration of progeny from a "source" cell to a "target" cell located at least the specified Euclidean distance from the source cell. Long-range migrations are only made if both source and target cells have the same dominant lineage, i.e. R, G, B, C, M or Y. It is assumed that progeny of the dominant lineage are the ones that migrate, and that migration reflects an increase in local competitive fitness.
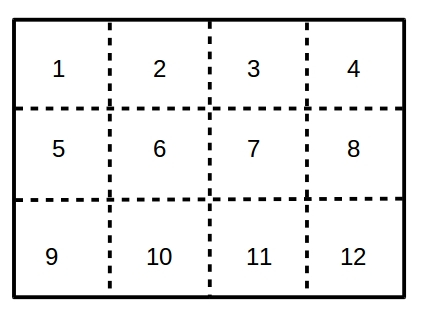
"Impose migration biases" assures that the specified fraction (default = 50%) of long-range migrations are between specific grid regions as shown in the diagram below: progeny from region 1 preferentially migrate to region 3, progeny from region 2 preferentially migrate to region 4, 5 to 7, 6 to 8, 9 to 11 and 10 to 12.

Increased reproduction by progeny of fitter lineages is modelled by increasing the fraction of the dominant lineage in the source cell by the competitive advantage ratio, specified as a ratio (default ratio = 0.2 so default competitive advantage ratio = 0.2 * 0.25 = 0.05) of the nearest-neighbor convergence rate, on each model iteration. The probability that the neoblasts undergoing these long range migrations will have a reproductive advantage in their target cell can be specified (default = 80%); in this case both source and target cells increase their dominant lineage by the specified competitive advantage ratio on each model iteration.
"Impose survival biases" enhances competitive advantage (default = 2x) of long-range migrants between particular 10 x 10 cell regions. The biases favor Red - Cyan - Red - Cyan in the top third of the grid, Green - Magenta - Green - Magenta in the middle third and Blue - Yellow - Blue - Yellow in the lower third. Migrants of all other lineages are disfavored by the same factor in each region. These biases model differences in compatibility between neoblast lineages and morphological regions, e.g. ability to correctly interpret region-specific morphological signals.
With the default parameter settings, no migration and no biases, the model converges toward uniformity, i.e. a completely gray display. Allowing migration with default parameters and no biases generally leads to a stable state in which different neoblast regions have "taken over" different areas of the grid. Increasing the migration probability increases the number and decreases the size of these areas.
Even with only 10% (default) migration probability, increasing the competitive advantage of lineages that produce migrating neoblasts to between 50% and 60% of the short-range conversion rate introduces instability, including multiple islands of runaway winner-take-all competition. Regional suvival biases interact with competitive advantage, and generally increase instability at a given competitive advantage setting.